我把刚才题的答案公布一下啊,只有40的解答是对的.真佩服她,这也能搜出来.我在网上找过,但找不到.
我解的方法是这样的,也象40一样,把球按编号123456789ABC.1234为第一组,5678为第二组,9ABC为第三组.
第一称:先将1234和5678称.此时天平出现情况1平衡,2不平衡
1平衡:那说明异常球在第三组----这是第一种情况。2不平衡----这就要用第二种情况.
针对第一种情况的称法.
第一称:先将1234和5678称.此时天平出现情况1平衡.
第二称:从第一组里拿两个球,从第三组里拿9和A两个球。此时出现两种情况1平衡,2失衡
1平衡:那说明异常球是B或C. 2不平衡:那说明异常球不是9就是A.
那么针对平衡情况的最后一称就是
第三称:拿球1和球B称.如果不平衡说明,异常球就是B,如果平衡那说明异常球就是C.
针对不平衡情况的最后一称就是
第三称:拿球1和球9称.如果平衡,那说明A是异常球.如果不平衡,那9就是异常球.
这是第一种情况的称法,一共三次.
接下来就是第二种情况了.
第一称:先将1234和5678称.此时天平出现情况2不平衡.
那说明:质量异常球就在这两组里,第三组球全部正常.这里我假设一下第一组重,第二组轻(反过来假设一样,反正肯定是一个重一个轻).
第二称:天平的A端放上第一组的123和第二组的5,B端放上第三组的9AB和第一组的4.此时出现的情况1平衡,2不平衡
1平衡,那说明不正常的球是678,而且可以断定不正常的球是轻---因为刚开始就是第一组重,第二组轻,但第二组的5球又是正常的,所以678里有一个轻的球.
那么平衡的最后一称就是
第三称(平衡):将6和7称,如果平衡,8重.如果不平衡,那谁重谁就是重球,也就是异常球.
2不平衡(1)A边重.那说明第4个球是正常的,因为刚开始就是第一组重,如果第4个球是重球,那么就应该是B边重.所以异常球,而且绝对是重球是在123.
这样的第三称就是
第三称(不平衡1)将1和2对称一下,谁重就是谁.如果平衡,那3就是重的异常球
不平衡(2)B边重,那就说明,不是4是重球就是5是轻球.因为刚开始第一组重,第二组轻.4属于第一组.5属于第二组.
那这样的第三称就是
第三称(不平衡2)将1和4称.如果平衡,那5就是轻球.如果4重,那4就是重的异常球.
以上方法全部都是只用称三次的.符合题目的要求.
这道题的难点在于:1、不知道球是重是轻.
2、在第一称出现不平衡之后.如何分配球---在这儿绝大数人想半天也会想不出来的,我是每样都试了才试出这样才可行的.而且用这种方法后,有几样情况是不可能出现的,所以这里也会迷惑很多人.
其它所有的回答均错误,原因一没好好理会题目的含义.二就是根本也没好好的深入的去想一下.哈.
[ 本帖最后由 Forcose 于 2006-12-8 22:45 编辑 ] |
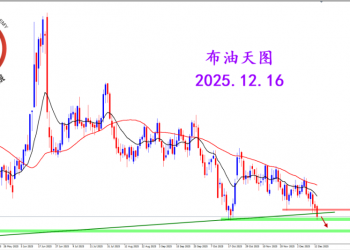 2025.12.16 图文交易计划:布油开放下行 关1655 人气#黄金外汇论坛
2025.12.16 图文交易计划:布油开放下行 关1655 人气#黄金外汇论坛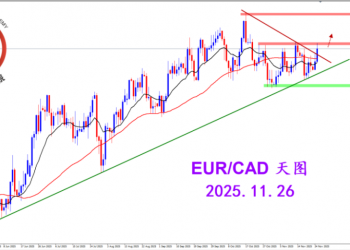 2025.11.26 图文交易计划:欧加试探拉升 关2956 人气#黄金外汇论坛
2025.11.26 图文交易计划:欧加试探拉升 关2956 人气#黄金外汇论坛 MQL5全球十大量化排行榜3029 人气#黄金外汇论坛
MQL5全球十大量化排行榜3029 人气#黄金外汇论坛 【认知】5818 人气#黄金外汇论坛
【认知】5818 人气#黄金外汇论坛